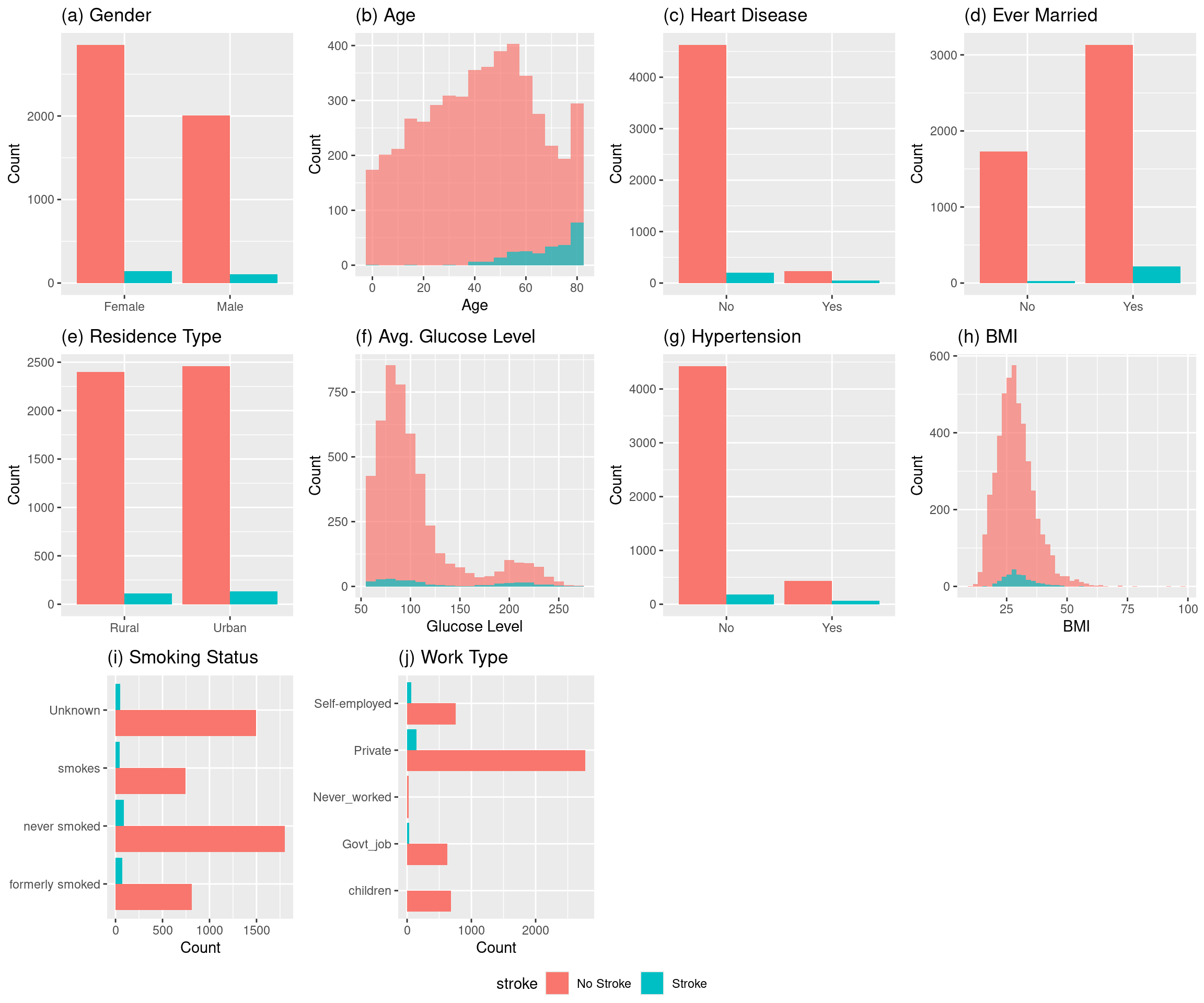
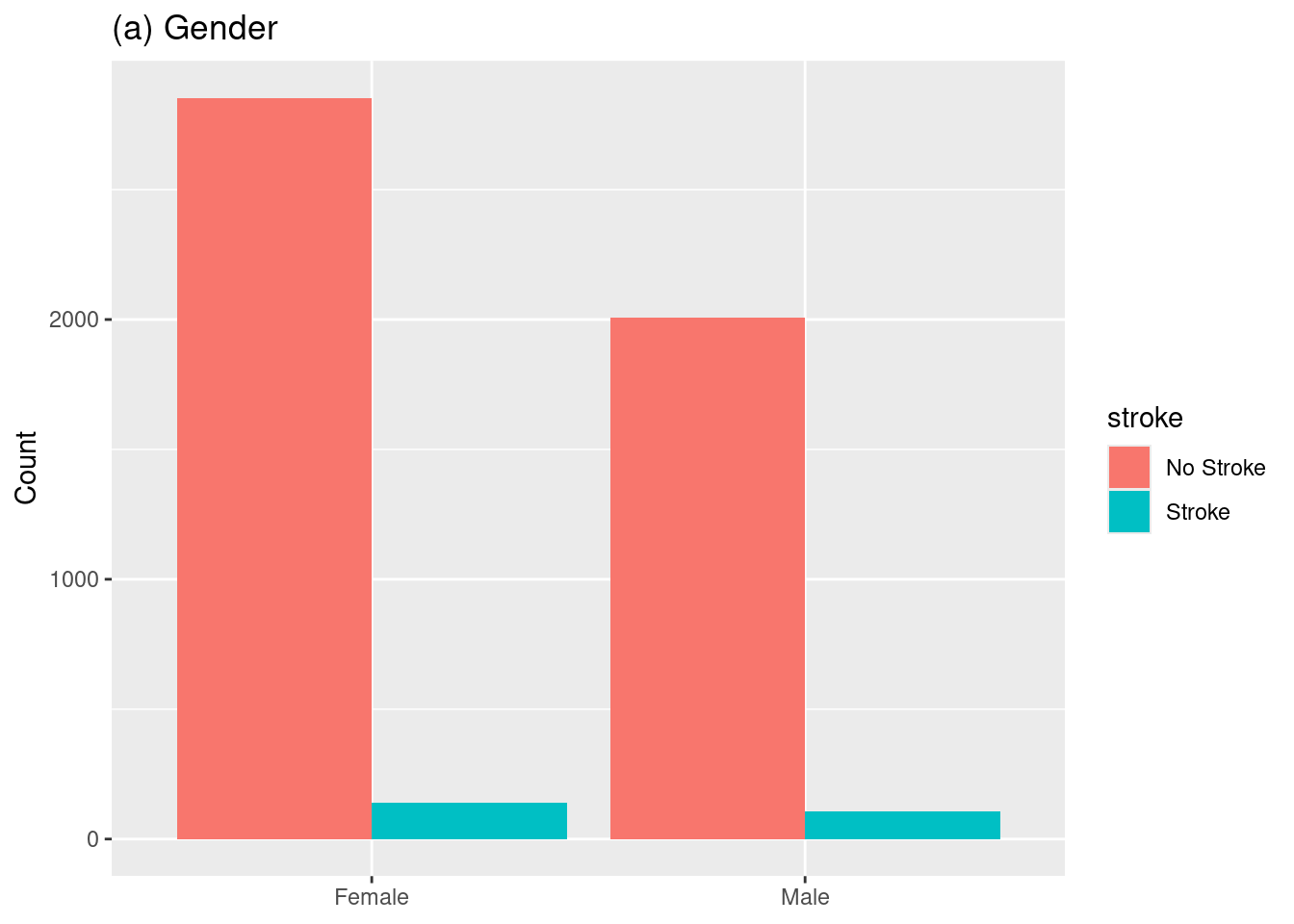
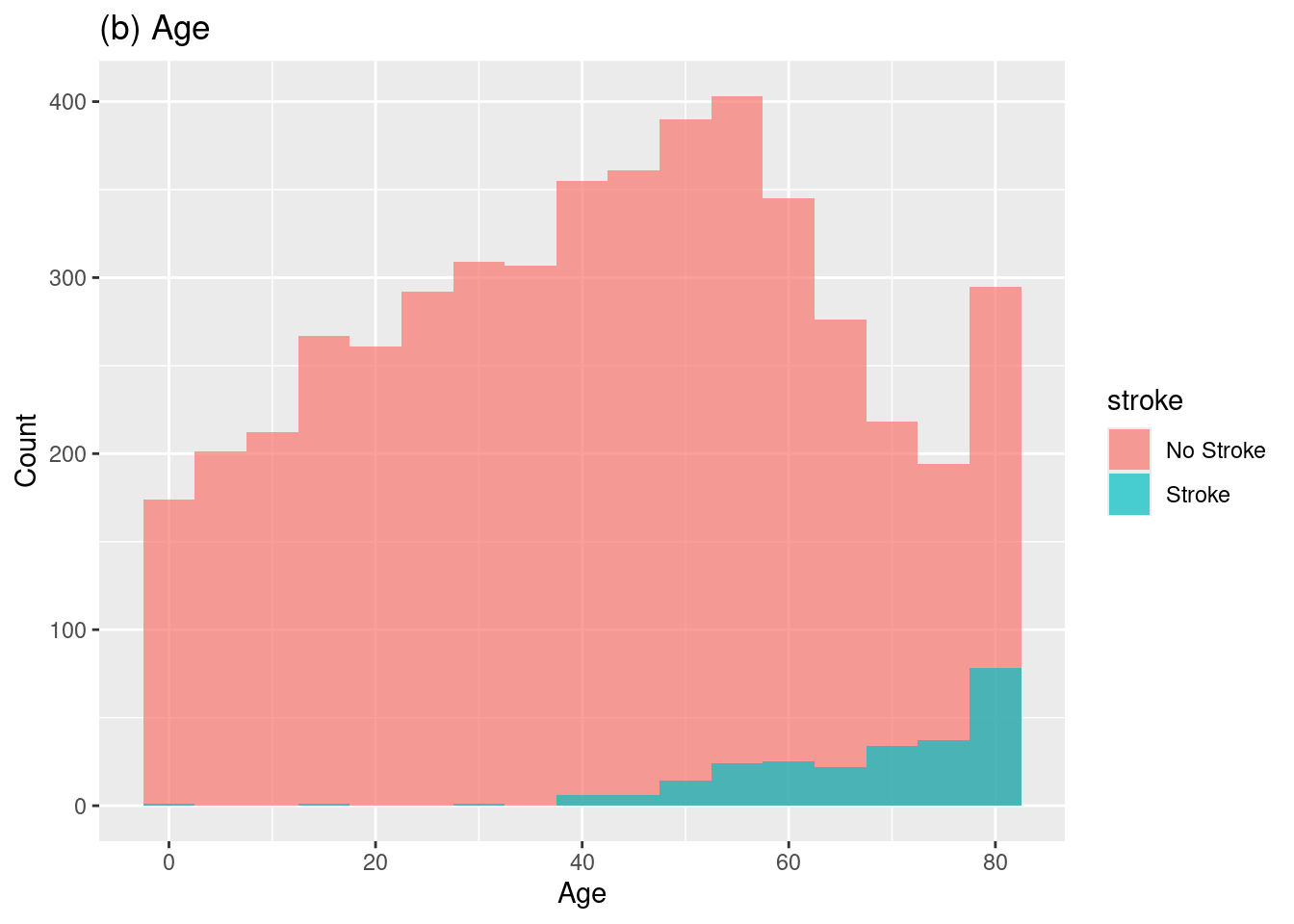
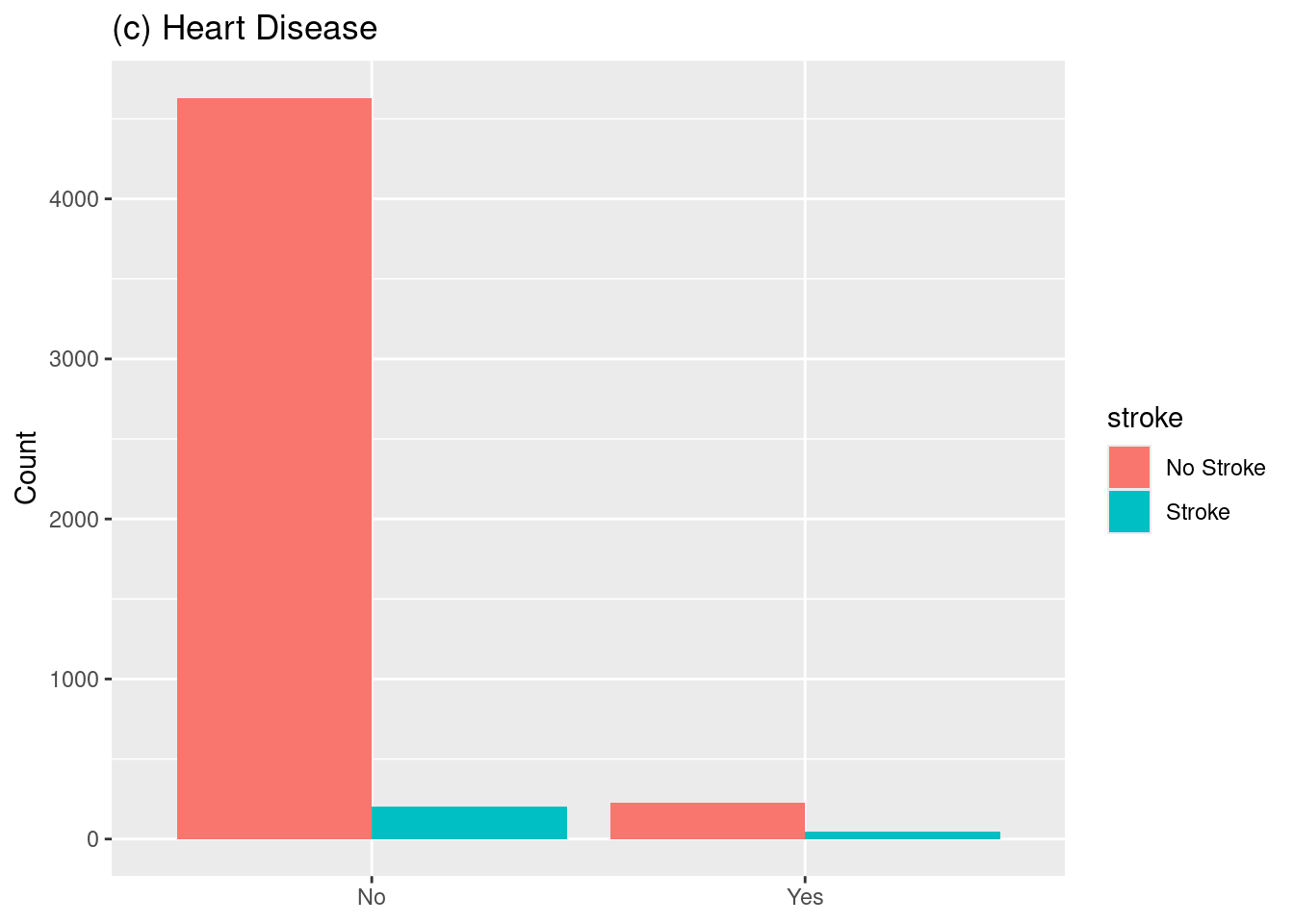
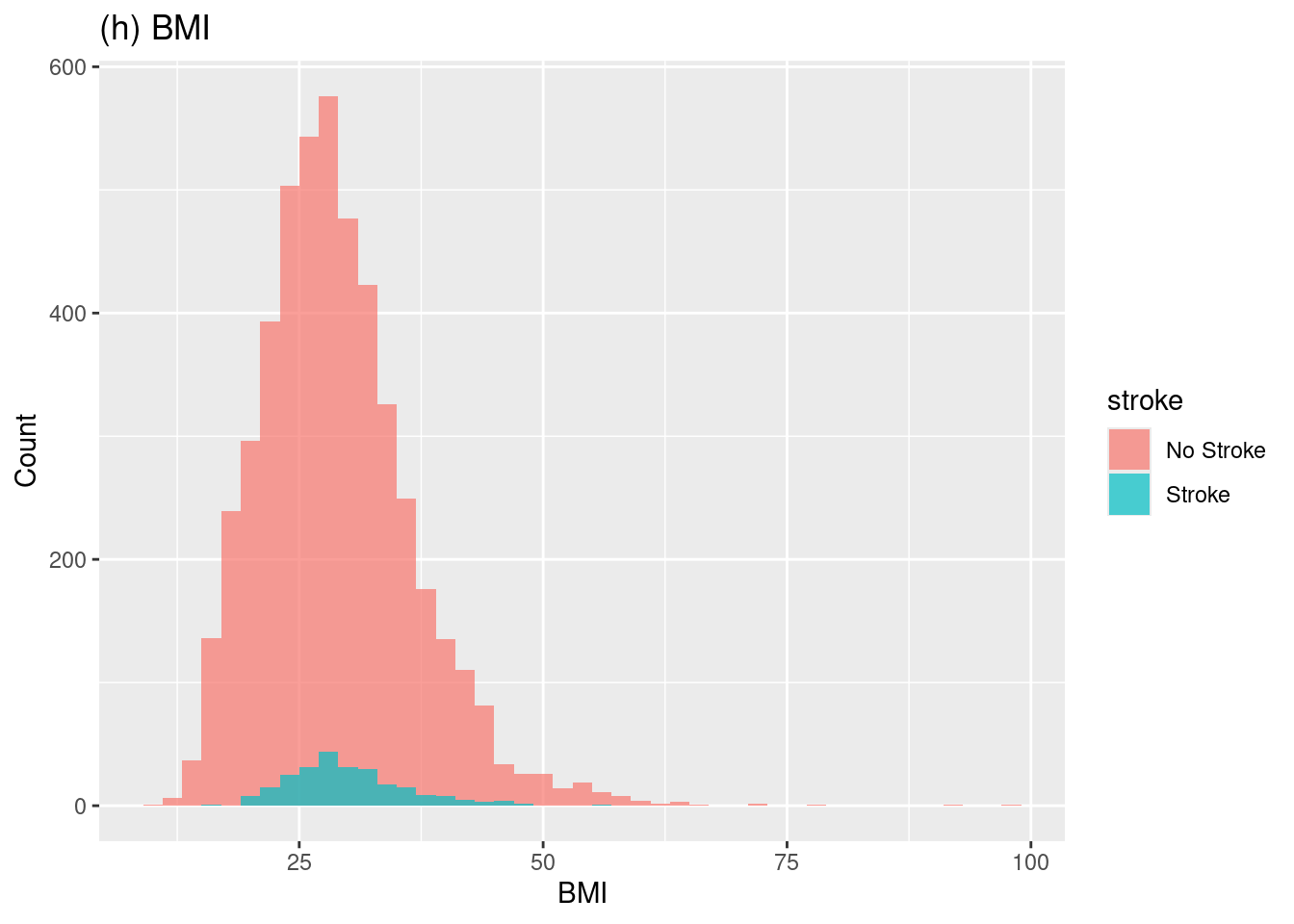
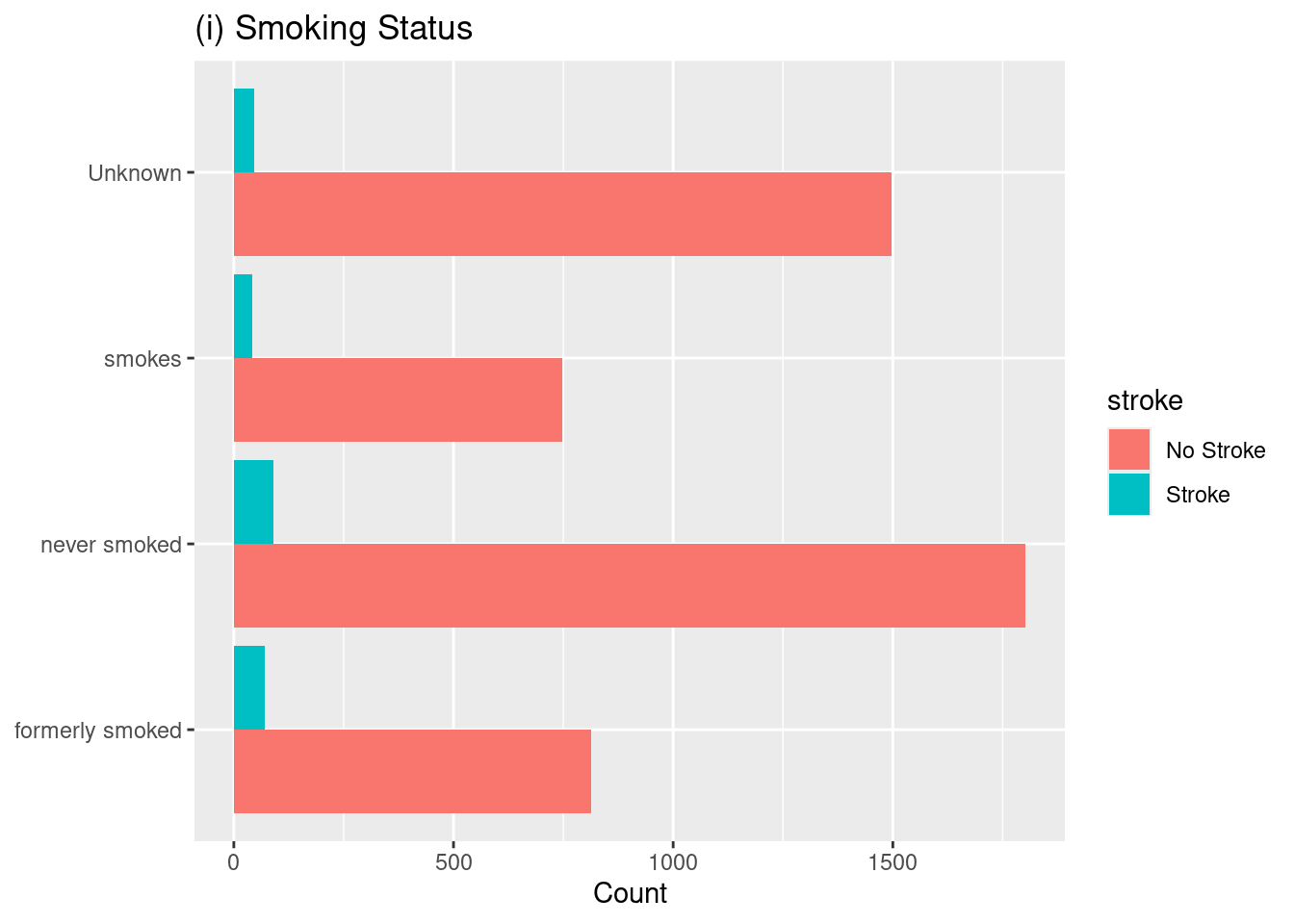
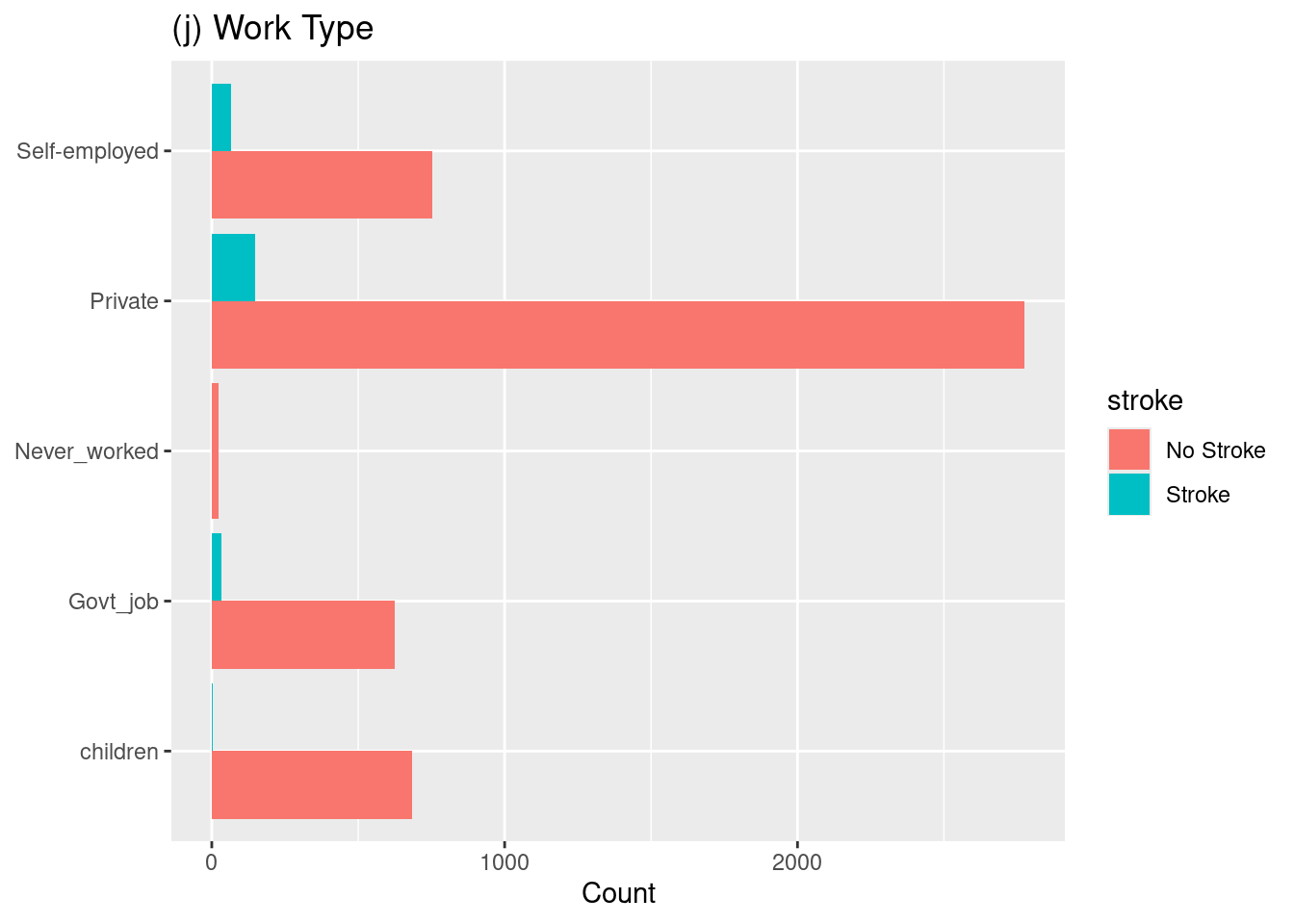
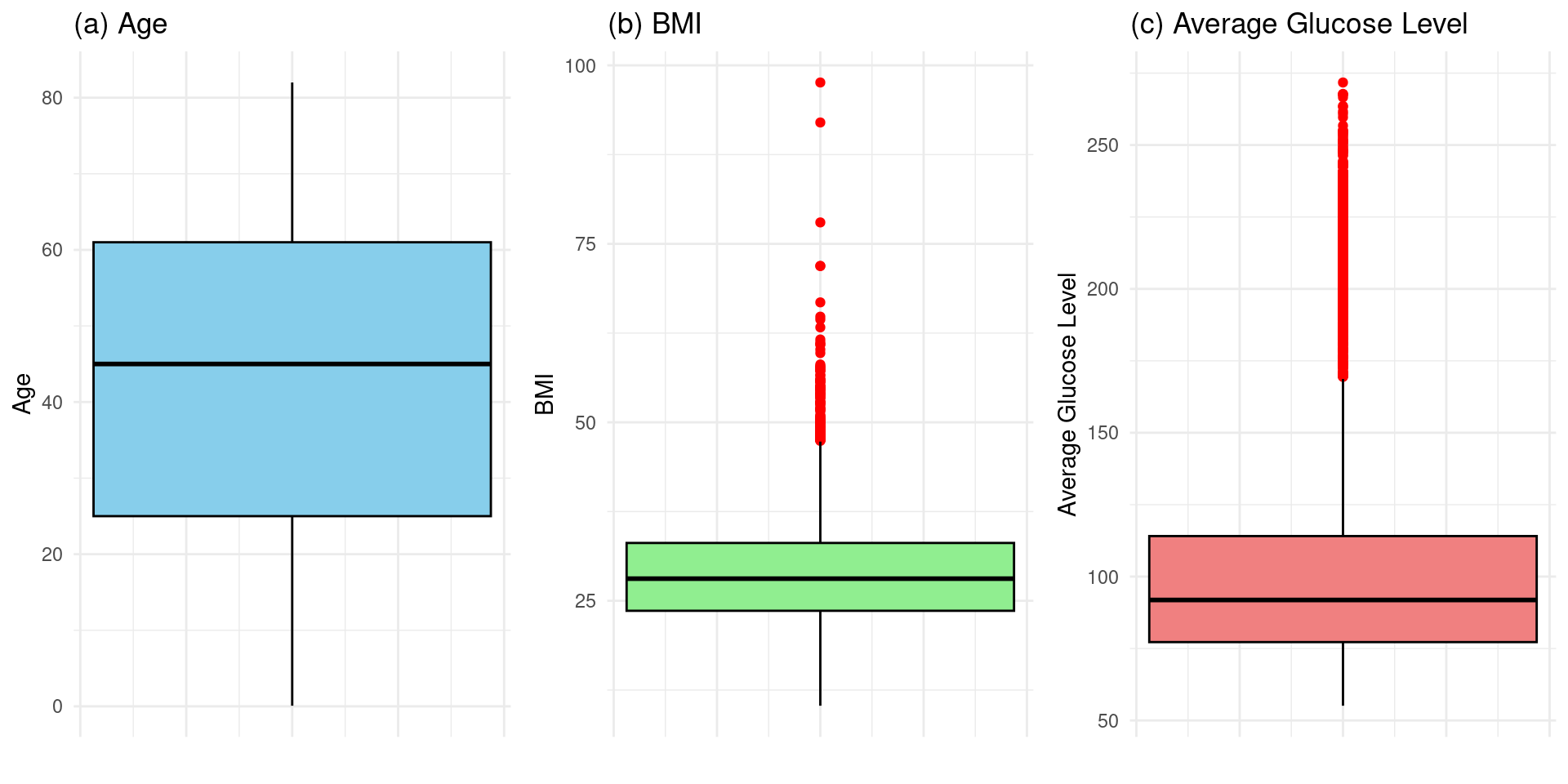
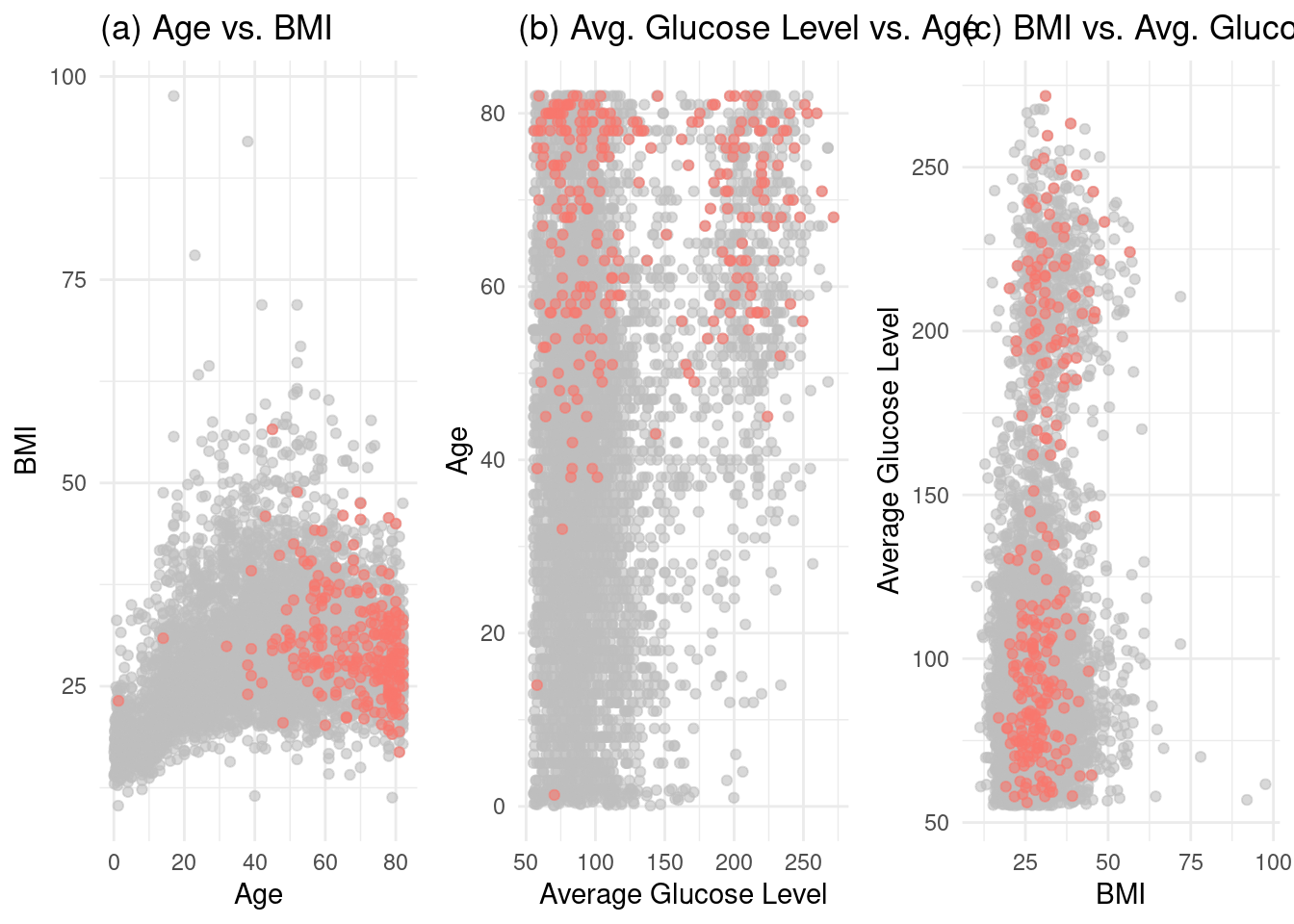
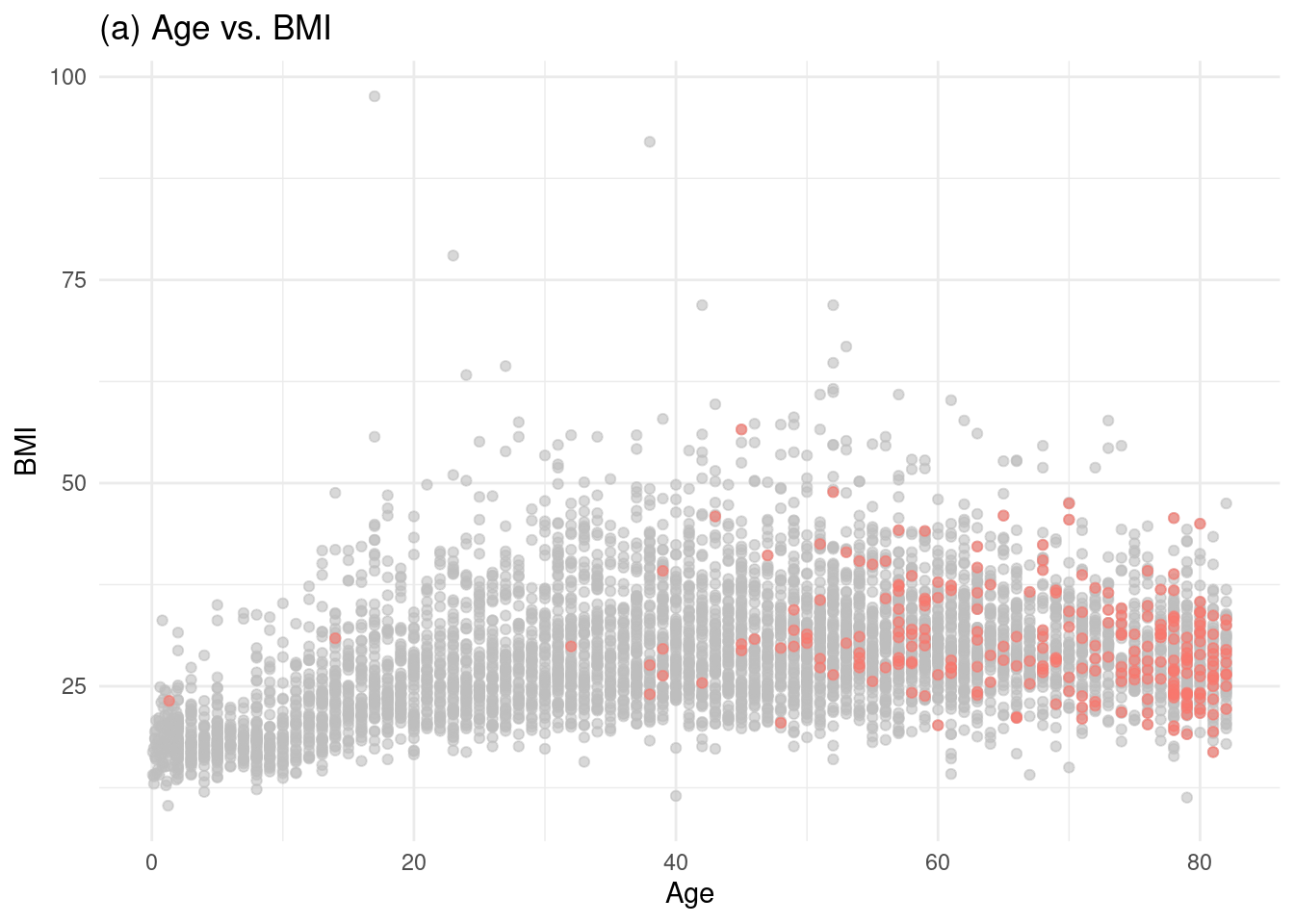
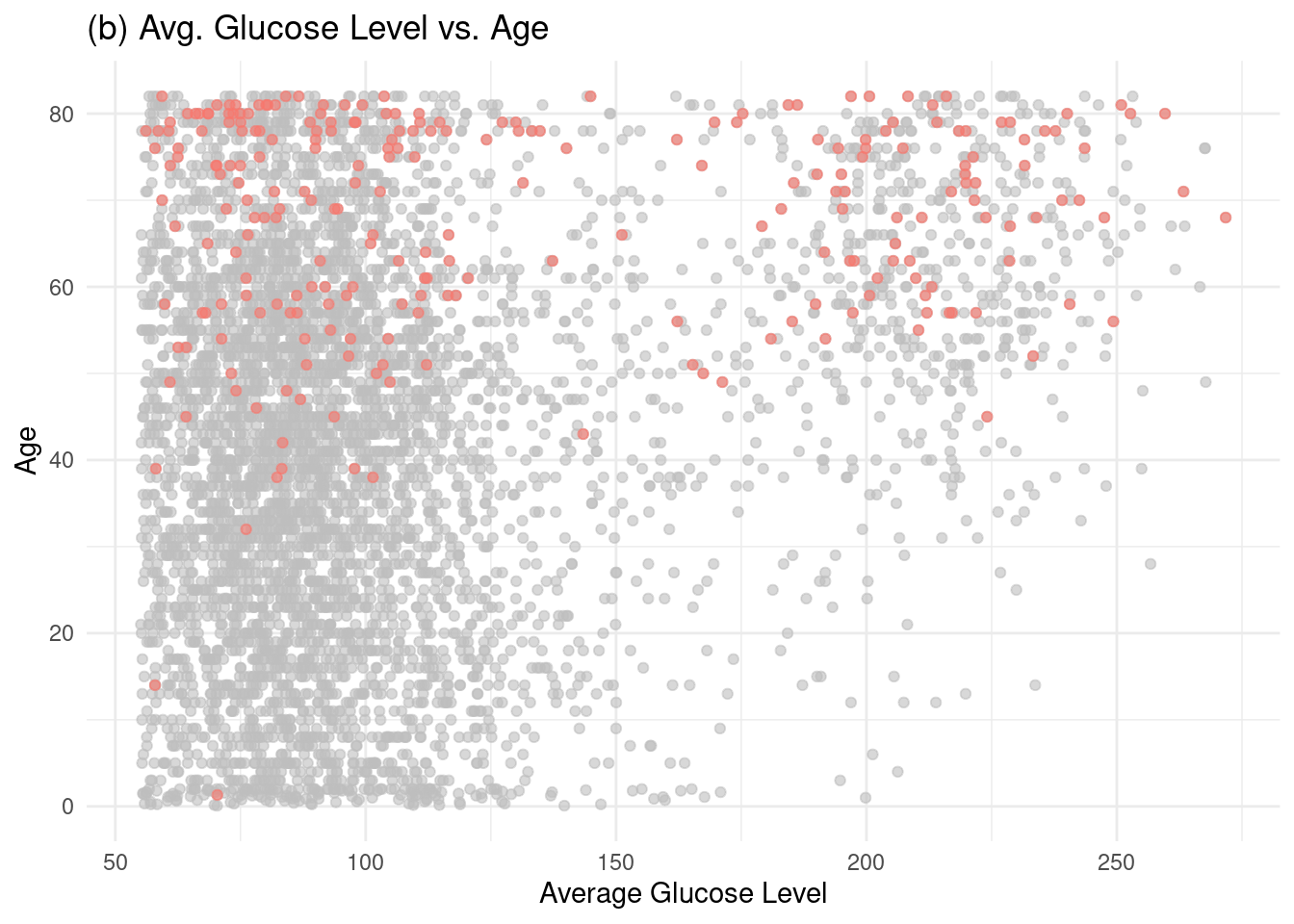
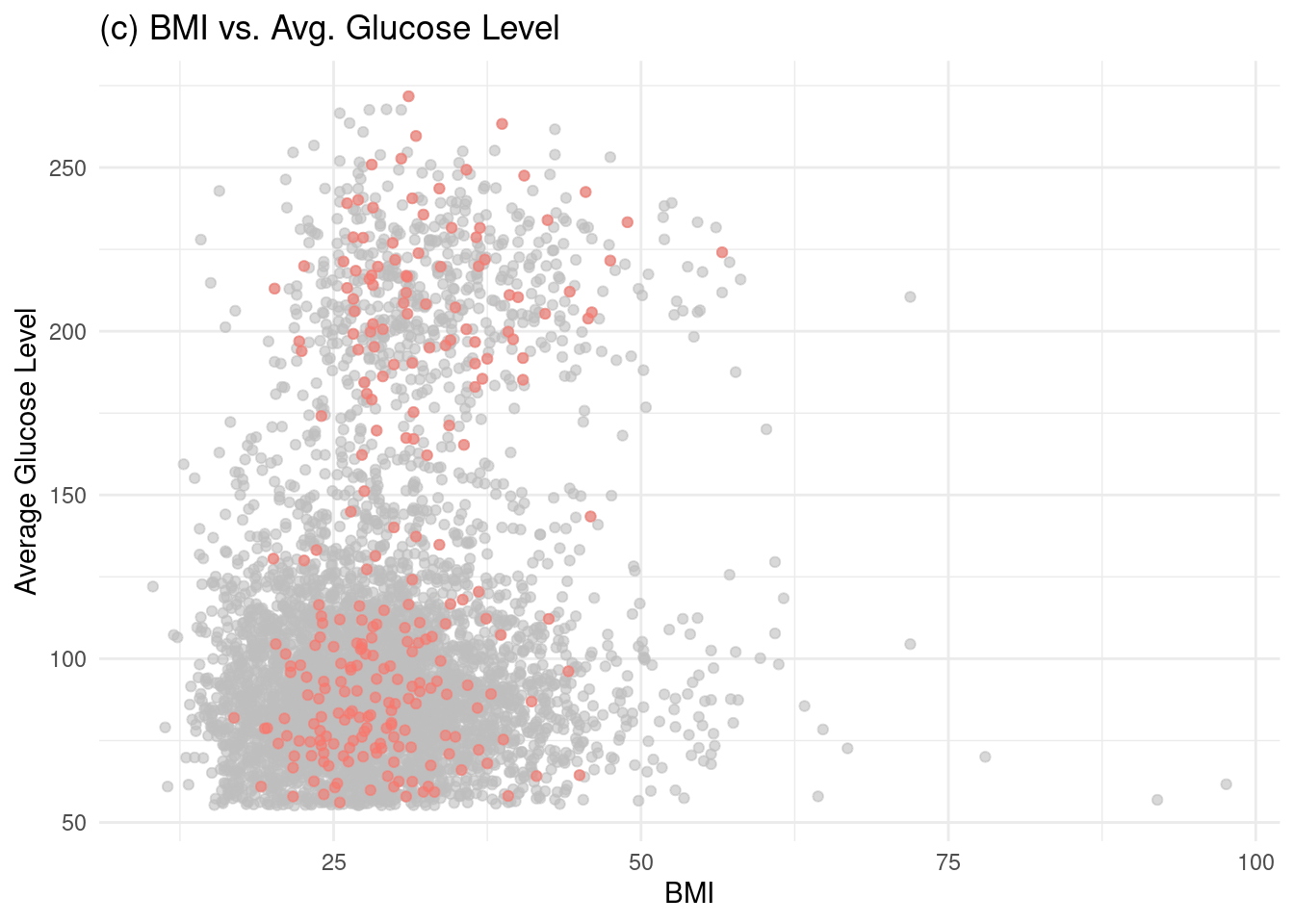
1. Hassan, A., Gulzar Ahmad, S., Ullah Munir, E., Ali Khan, I., & Ramzan, N. (2024). Predictive modelling and identification of key risk factors for stroke using machine learning. Scientific Reports, 14(1), 11498.
2. Kokkotis, C., Giarmatzis, G., Giannakou, E., Moustakidis, S., Tsatalas, T., Tsiptsios, D., Vadikolias, K., & Aggelousis, N. (2022). An explainable machine learning pipeline for stroke prediction on imbalanced data. Diagnostics, 12(10), 2392.
3. Sirsat, M. S., Fermé, E., & Câmara, J. (2020). Machine learning for brain stroke: A review. Journal of Stroke and Cerebrovascular Diseases, 29(10), 105162.
4. Wongvorachan, T., He, S., & Bulut, O. (2023). A comparison of undersampling, oversampling, and SMOTE methods for dealing with imbalanced classification in educational data mining. Information, 14(1), 54.
5. Sowjanya, A. M., & Mrudula, O. (2023). Effective treatment of imbalanced datasets in health care using modified SMOTE coupled with stacked deep learning algorithms. Applied Nanoscience, 13(3), 1829–1840.